コンピュータビジョンの分野における3次元復元は,物体の立体形状を復元する技術です.レーザなどを照射して高精度に立体形状を計測することもできますが,デジカメなどで撮影された写真のみから立体を復元できると手軽に3次元データを利用することができるようになります.ここでは,画像のみを用いた3次元復元について紹介します.
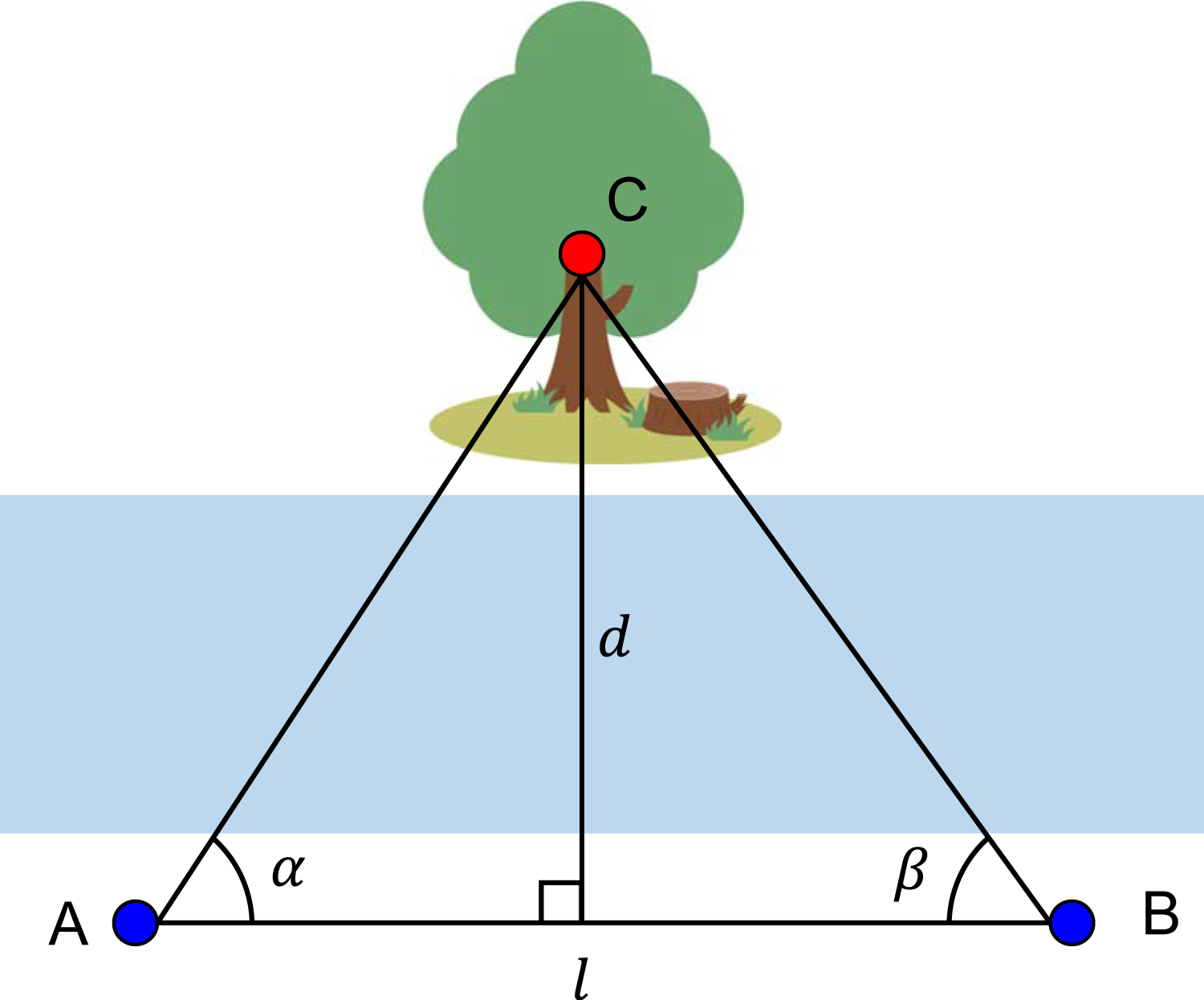
「三角測量」という言葉を聞いたことがあるでしょうか?数学の授業で図 1 のように対岸の木までの距離を計測する例で紹介されていると思います.同じ側にある点を $A$ と $B$ とし,対岸の木を $C$ とします.このときに,$AB$ 間の距離 $l$,$\alpha = \angle CAB$,$\beta = \angle CBA$ がわかれば,対岸の木までの距離 $d$ を求めることができます.三角比を用いると距離 $d$ は次式で求められます. \[ d = \frac{l}{\frac{1}{\tan\alpha}+\frac{1}{\tan\beta}}=\frac{\sin\alpha\sin\beta}{\sin(\alpha+\beta)}l \] 左側の直角三角形について $\tan\alpha$ を,右側の直角三角形について $\tan\beta$ を考えると $d$ の式が導出できます.三角測量の原理を使って画像から立体形状を復元する技術をステレオビジョンと呼びます.
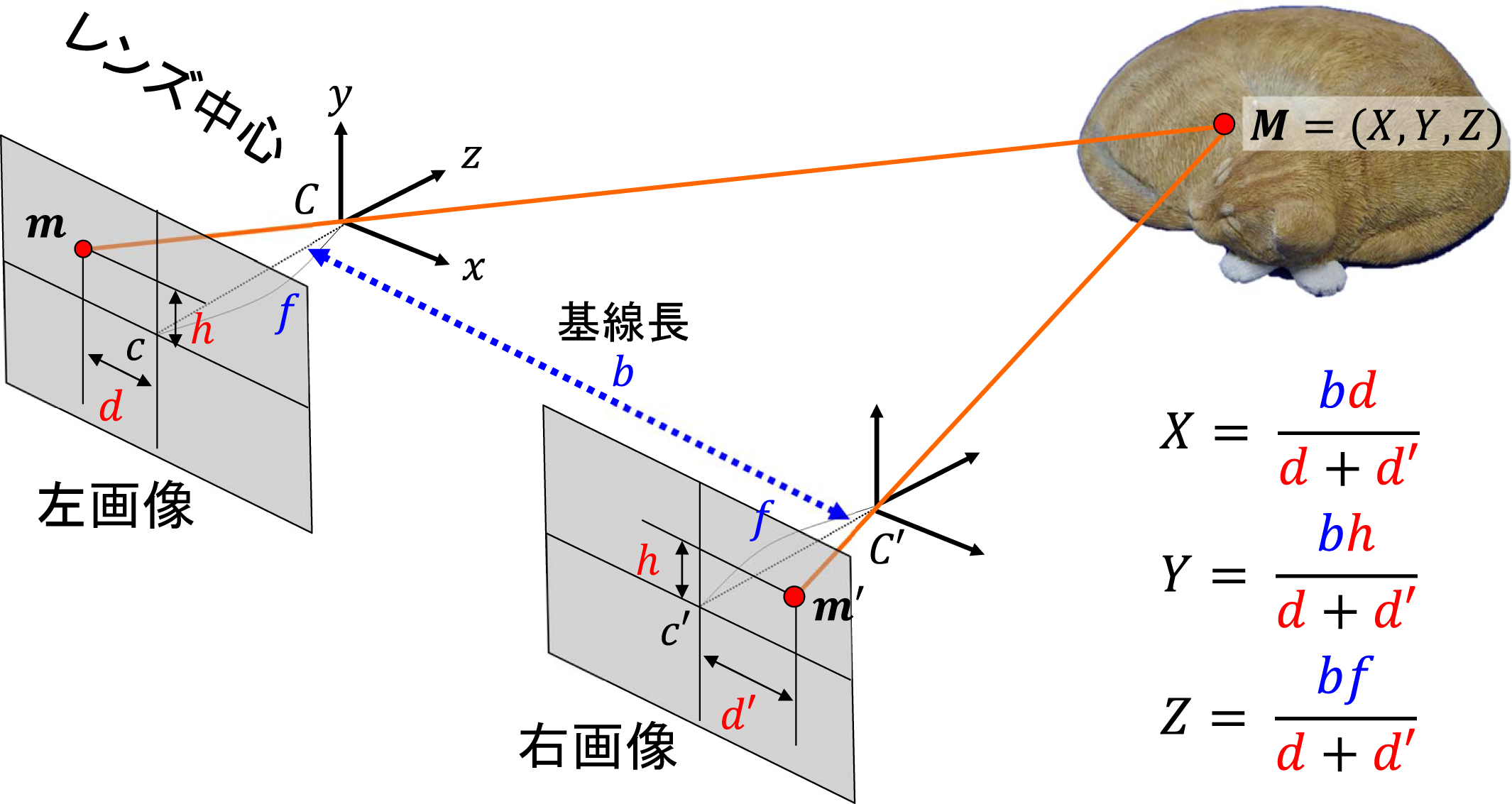
ステレオビジョンは,図 2 のように,2 台のカメラを使って物体の立体形状を復元する技術です.三角測量と比べると変数が増えています.ステレオビジョンでは,物体がカメラ画像にどう写るかを示す投影モデルを利用するためです.このときに重要となるのがカメラパラメータと呼ばれるカメラの特徴を示すパラメータです.カメラパラメータには 2 種類あります.1 つめは内部パラメータです.これは,カメラ自身の特徴を表すパラメータで,画像中心座標 $c$,レンズ中心座標 $C$,焦点距離 $f$ などで構成されます.もう 1 つは外部パラメータです.2 台のカメラを使うので,カメラ間の相対的な位置関係(平行移動と回転など)が必要になります.図 2 であれば,カメラ間の距離を示す基線長 $b$ になります.左画像上の点 $m$ と右画像上の点 $m'$ が対象物体の同じ位置を示しているとき,図 2 の式を使って物体の 3次元位置 $M$ を求めることができます.画像を構成する全ての画素に対して同様な計算をすることで,物体の詳細な立体形状を復元することができます.少し複雑そうに感じるかもしれませんが,基本的な原理は三角測量になります.
本研究室で開発したデジカメを使った3次元復元システムを紹介します.デジカメで2枚以上の写真を撮ると対象物体の立体形状を復元することができます.詳細については,文献 [1] や [2] を参照して下さい.動画1は,本システムのデモ動画です.何枚か写真を撮影してノートパソコンに写真が転送されると立体形状が復元されます.さらに写真を追加で撮影すると,物体の全体が復元されていくのがわかります.
2枚の画像から立体形状を復元するステレオビジョンに対して,複数枚の画像から立体形状を復元する技術を多視点ステレオと呼びます.物体全体を画像に納めると,見えていない箇所の形状を復元することができません.物体周辺を複数回撮影した画像を使うことで,物体全体の立体形状を復元することができます.動画2は,202枚の多視点画像とそれらの画像から復元した立体形状です.たくさんの画像を入力として使うことで,物体の詳細な形状を復元することができます.
画像は,3次元空間のシーンを2次元平面に投影することで得られます.このとき,画像の1画素と3次元空間の1点との間を直線で対応づけていると考えることができます.この直線を「光線」と呼びます.3次元シーンと画像との間にたくさんの光線があり,それで画像が構成されています.このたくさんの光線を深層学習で推定する手法がNeural Radiance Fields (NeRF)です.NeRFを推定することができれば,そのシーンを任意の視点から撮影したような画像を作ることができます.光線を推定する過程でカメラから物体までの距離(深さ)を求めているので,NeRFを用いることでデプスマップと呼ばれるカメラから物体までの深さのマップを求めることができます.多視点ステレオは物体表面の詳細な形状を復元することができ,NeRFは物体境界を正確に復元することができます.現在,文献[5]や文献[6] のように多視点ステレオをNeRFを組み合わせた新しい手法を検討しています.
本研究室で取り組んでいる3次元復元に関する研究で得られた成果の一部を紹介します.




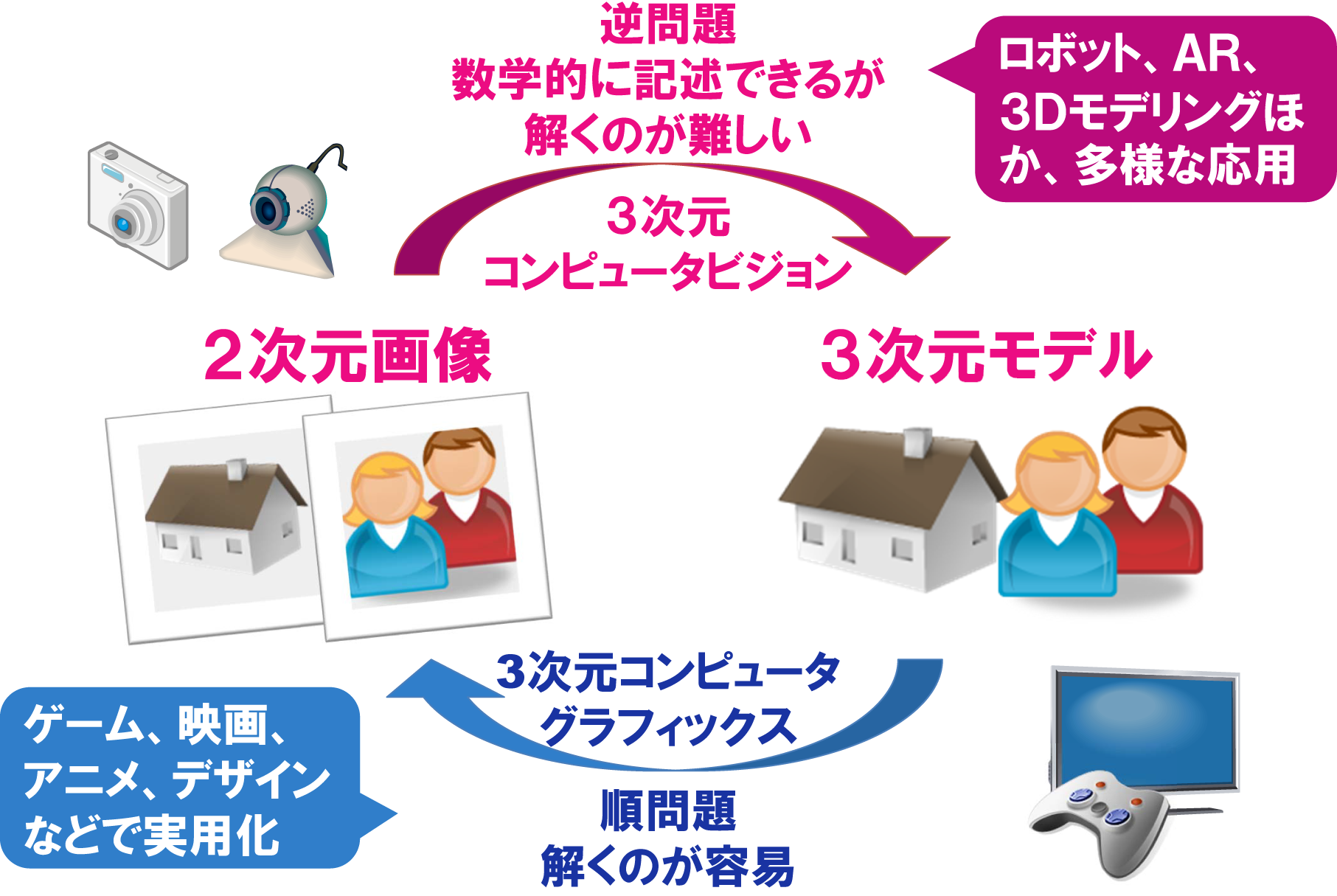
簡単ではありますが,3次元復元の研究について紹介しました.3次元復元は,図6のように逆問題になります.私たちがいるのは3次元空間なので,物体は立体形状を持っています.例えば,それを2次元の画像として記録するのが写真撮影です.立体(3次元)を画像(2次元)にするので順問題であり,簡単に解くことができます.ゲームも同様です.3次元モデルをテレビに表示しているので3次元を2次元にしています.3次元復元は,その逆問題を解くことに相当します.2次元で表現された画像から3次元を求めるので,数学的な計算モデルはありますが,解くためには,いろいろな工夫が必要となります.これまで紹介してきたように,画像から立体形状を復元することができれば,いろいろな応用が検討できます.そのため,コンピュータビジョンの分野では,この難問題を多くの研究者が取り組んでいます.